这是黄文森的个人介绍网页
欢迎访问!
基本信息
出生日期:2001.01.29
TEL:19951111301
Email:1228834350@qq.com
户籍:江苏省苏州市
教育背景
2023.09-今
中南大学数学与统计学院
数学专业(硕士研究生)
2019.09-2023.06
南京审计大学数学与统计学院
金融数学专业(本科)
参与项目
- 实证金融分析
- 期权的期货复制策略研究
- 邮件自助收发系统
- Online文件生成+数据库归档
- 在险价值Var的GARCH模型估计
- 自动化签到Script
- Bilibili弹幕爬虫+自然语句分析
- 本地推理模型+数据库处理
参与项目(代码展示在下方)
01.
实证金融分析-投资组合建立
分析历史金融数据,实现对于交易价格波动性的分析。从证券网站下载历史数据导入到Dataframe,分配数据整理工作,计算指标分析,基于均值方差构建CAPM模型。
02.
邮件收发系统
独立完成了基于POP3和SMTP协议的邮件发送和下载分析工作,用于接受收到的课程结课作业。编写了邮箱服务器登陆模块,实现了邮箱接受图片和附件。基于正则表达式和课程名单的匹配,分析邮件内容。收到邮件后自动回复固定格式文字邮件。
03.
期权的期货复制与套利策略研究
度量高频交易数据下的波动率,利用高频交易数据提高套利收益。使用ARIMA时间序列模型预测,基于历史波动率及时间序列模型捕捉到的A种波动率,构造出A^2种不同策略,比较所构造策略的收益。
04.
Online文件生成
接受固定格式的数据录入,传入本地数据库,接入后台的python自动化word操作模块,将对应位置填写为网页端填写数据,打印为PDF后提供下载。同时留存一份,按需排序后合并为一张PDF再打印
05.
在险价值VaR的GARCH模型估计
估计在险价值Var,基于IGarch(1,1)和t分布Garch模型,预测未来的在险价值,使用已有数据回测保证模型正确性。
06.
小额贷款信用风险评价
基于lg二元回归对用户的逾期风险进行预测,使用支持向量机SVM和FNN神经网络训练数据集,得出贷款用户风险评估。
07.
自动化签到Script
基于python的,通过adb协议控制桌面安卓模拟器的程序,通过构建本地网络映射端口的adb服务避免与桌面安卓模拟器的adb连接冲突。
此项目实现了在windows端对安卓模拟器的自动化操作,可以自动签到。图片模块对比的CV2模块匹配速度慢,正确率低,后安装百度的开源轻量化飞浆Paddle轻量化模型进行本地文字OCR识别,提高正确率和匹配速度。
08.
Bilibili弹幕爬虫+自然语句分析
B站弹幕为固定视频网址附加特定格式后缀可访问网站,使用Python爬虫程序可读取弹幕&发送时间,分析频率,制作词云图。
此项目在不访问视频文件时实现词云分析,减少了被反爬虫机制拦截分险。
09.
本地推理模型+数据库处理
在本地安装轻量化推理模型,对于使用正则表达式难清洗的数据,生成映射表,结合python+Mysql,实现了收到的大量复杂文件的清洗,分组,重命名等操作。
PART1:清洗提取数据
import pandas as pd
import numpy as np
# 读入5分钟数据
data_5min = pd.read_csv("HS300指数5min(2010.1.1_2021.10.31).csv",encoding='gbk')
# 读入日数据
data_day = pd.read_csv("HS300指数day(2010.1.1_2021.10.31).csv",encoding='gbk')
data_5min.head()
data_day.head()
data_5min['时间'] = pd.to_datetime(data_5min.时间, format='%Y/%m/%d %H:%M') # 将数据data_5min时间转换为Datetime格式
data_day['时间'] = pd.to_datetime(data_day.时间, format='%Y/%m/%d') # 将数据data_day时间转换为Datetime格式
print(data_5min.head())
data_5min['时间_年月日'] = data_5min.时间.dt.strftime('%Y-%m-%d') # 提取高频数据年月日时间,并作为一列向量存储在data_5min数据中,该列名称为'时间_年月日'
print(data_5min.head())
data_5min['时间_年月日'] = pd.to_datetime(data_5min.时间_年月日, format='%Y-%m-%d')
data_5min['时间_年'] = data_5min['时间'].dt.year # 提取年时间,并作为一列向量存储在data_5min数据中,该列名称为'时间_年'
print(data_5min.head())
# 匹配高频数据与日数据的年月日时间是否相同
data_day['时间_5min'] = np.unique(data_5min['时间_年月日']) # 按顺序提取高频数据中不同的日期,并放入日数据集中
data_day['时间_5min'] = pd.to_datetime(data_day.时间_5min, format='%Y-%m-%d') # 将高频数据的日期变为datetime格式
# 匹配高频数据与日数据的日期是否相同,相同为0,不同为1,进行加总
sum_different = np.where(data_day['时间'] == data_day['时间_5min'],0,1).sum()
print('高频数据与低频数据不同的日期数量:',sum_different)
data_day.head()
data_5min.head()
freq = data_5min['时间_年月日'].value_counts() # 统计高频数据中不同日期的数据量
print(freq)
freq.sort_index(inplace=True) # 按照index日期排序,默认为升序,inplace=True表示在原数据上进行操作
#freq[freq<48] # 查看小于48条数据的日期
#print(freq)
print(sum([freq<48]))
np.where(freq<48,1,0).sum()#查看有缺失数据的天数,条件freq<48成立为1,不成立为1,进行加总
import matplotlib.pyplot as plt
fig = plt.figure(figsize=(10,8)) #设置图像尺寸大小
plt.plot(freq,linewidth=1) #画出每天数据的个数
plt.xlabel('时间',fontsize=24)
plt.ylabel('每天样本个数',fontsize=24)
plt.title('每天数据图',fontsize=24)
plt.show()#显示图像
date_high = data_5min['时间'] # 高频数据时间
date_low = data_day['时间'] # 日数据时间
data_high = data_5min['收盘价'] # 高频数据收盘价
data_low = data_day['收盘价'] # 低频日数据收盘价
diff = np.diff(np.log(data_high)) ** 2 # 高频数据对数差分的平方
# 计算RV1
RV = []
rv1 = diff[0:freq[0]-1].sum() * (48/47)#计算第一天的RV
RV.append(rv1)
n1 = freq[0] - 1
# 计算RV
for i in range(1,len(freq)):
rv = diff[n1:(n1+freq[i])].sum() * (48/freq[i])
RV.append(rv)
n1 += freq[i]
# 对于一天数据量较少的RV进行处理,对于数据量少于ratio的RV直接用前一天来代替
ratio = 0.5
for i in range(len(freq)):
if freq[i] < np.mean(freq)*ratio:
RV[i] = RV[i-1]
# 计算RV_week
RV_week = []
for i in range(len(RV)-4):
rv_week = sum(RV[i:(i+5)]) / 5
RV_week.append(rv_week)
# 计算RV_mon
RV_mon = []
for i in range(len(RV)-21):
rv_mon = sum(RV[i:(22+i)]) / 22
RV_mon.append(rv_mon)
# 计算RV_3mon
RV_3mon = []
for i in range(len(RV)-65):
rv_3mon = sum(RV[i:(66+i)]) / 66
RV_3mon.append(rv_3mon)
diff_ma = np.diff(np.log(data_low)) # 日收益,即对数价格的查分
var_ma_his = [] # 方差
sig_ma_his = [] # 标准差,波动率
data_day[‘year_high’] = data_day[‘时间_5min’].dt.year #
len_year1 = len(data_day[data_day[‘year_high’] == min(data_day[‘year_high’])]) # 计算第一年后的数据长度
# 基于一个月的日收益率数据计算其样本方差、样本标准差,得到日波动率估计值
for i in range(len(diff_ma) – 22):
var_ma_his.append(np.var(diff_ma[i:22 + i]))
sig_ma_his.append(np.sqrt(np.var(diff_ma[i:22 + i]) * len_year1))
# 计算真实值
diff_ma_real = diff_ma[1:len(diff_ma)]
var_ma_real = []
sig_ma_real = []
for i in range(len(diff_ma_real) – 21):
var_ma_real.append(np.var(diff_ma_real[i:22 + i]))
sig_ma_real.append(np.sqrt(np.var(diff_ma_real[i:22 + i]) * len_year1))
print(len_year1)
import scipy.stats as stats
from statsmodels.stats.diagnostic import acorr_ljungbox as lb_test
def data_outline(x): # 自编描述性统计量,包含了均值、标准差、极差、偏度、峰度等特征
# x – list
n = len(x)
m = np.mean(x)
v = np.var(x)
s = np.std(x)
m1 = max(x)
m2 = min(x)
me = np.median(x)
cv = 100 * s / m
css = sum([(i – m) ** 2 for i in x])
R = max(x) – min(x)
R1 = np.percentile(x, 75) – np.percentile(x, 25) # 75%分位数-25%分位数
g1 = stats.skew(x) # 偏度
g2 = stats.kurtosis(x) # 峰度
tes = stats.jarque_bera(x).statistic # JB检验统计量,检验数据是否服从正态分布
p1 = stats.jarque_bera(x).pvalue # JB检验p值
q = lb_test(x, lags=11)[0][-1] # LB检验统计量,检验数据是否相依
p2 = lb_test(x, lags=11)[1][-1] # LB检验p值
return [m, me, m1, m2, s, g1, g2, tes, q, n], [p1, p2]
# a,b = data_outline(RV)
t0,p0 = data_outline(diff_ma)#日收益率标准差的描述性统计结果
t1,p1 = data_outline(RV) #日已实现波动率的描述性统计
t2,p2 = data_outline(RV_week)#周已实现波动率的描述性统计
t3,p3 = data_outline(RV_mon)#月已实现波动率的描述性统计
t4,p4 = data_outline(RV_3mon)#季度已实现波动率的描述性统计
t5,p5 = data_outline(np.log(RV))#对数日已实现波动率的描述性统计
t6,p6 = data_outline(np.log(RV_week))#对数周已实现波动率的描述性统计
t7,p7 = data_outline(np.log(RV_mon))#对数月已实现波动率的描述性统计
t8,p8 = data_outline(np.log(RV_3mon))#对数季度已实现波动率的描述性统计
print(t0,p0)
PART2:基于ARIFIMA时间序列的日周月季预测
#计算Hurst指数,用于估计ARFIMA(p,d,q)的分整阶数d,d=Hurst-0.5
# ARFIMA(p,d,q) -- d = Hurst-0.5
from pandas import Series
from __future__ import division
from collections import Iterable
def calcHurst(ts):
if not isinstance(ts, Iterable): # 检验输入变量ts是否是可迭代对象,数组、字符串、列表等都为可迭代对象
print('error')
return
m_min, m_max = 2, len(ts) // 3 # 确定组的个数,M
RSlist = []
for cut in range(m_min, m_max):
children = len(ts) // cut # 每组样本的个数n
children_list = [ts[i * children:(i + 1) * children] for i in range(cut)] # 将样本分成cut部分,每个部分含有children个样本
L = [] # 建立用于存储R/S统计量的列表L
for a_children in children_list:
Ma = np.mean(a_children) # 对子样本a_children取均值
Xta = Series(map(lambda x: x - Ma, a_children)).cumsum() # 对子样本a_children中心化后,进行累积求和
Ra = max(Xta) - min(Xta) # 计算数据Xta的极差
Sa = np.std(a_children) # 计算数据a_children的标准差
rs = Ra / Sa
L.append(rs)
RS = np.mean(L)
RSlist.append(RS) # 将RS统计量值加到RSlist
return np.polyfit(np.log(range(2 + len(RSlist), 2, -1)), np.log(RSlist), 1)[0] # 利用polyfit进行线性回归(1次多项式),估计hurst指数
from scipy.special import gamma # 导入gamma函数
from pandas import Series
import numpy as np
def calcy_d(ts, d):
n = len(ts) # 确定进行分数阶差分的序列的长度
ki = [] # 用于存储分数阶差分的系数的分量
ki.append(1)
for i in range(1, n + 1):
a = (i – 1 – d) / i
ki.append(a)
g = Series(ki).cumprod() # 分数阶差分的系数
y = [] # 用于存储分数阶差分序列
y.append(ts[0]) # 将时间序列ts的第一个数据
for i in range(1, n):
pi = g[0:i + 1] # 提取分数阶差分系数
yii = list(ts[0:i + 1]) # 提取时间序列ts的子样本,并且保存文
yii.reverse() # 将yii给逆序
yi = np.array(pi).dot(np.array(yii)) # 计算时间序列ts的
y.append(yi)
return y, g
from statsmodels.tsa.arima.model import ARIMA
#from statsmodels.tsa.arima.model import ARMA
from pmdarima.arima import auto_arima
print(data_day)
data_day[‘year_high’] = data_day[‘时间_5min’].dt.year#将data_day的列时间_5min的年份信息存入列year_high中
len_year1 = len(data_day[data_day[‘year_high’] == min(data_day[‘year_high’])]) # 计算第一年的数据长度
d = calcHurst(np.log(RV[0:len_year1])) – 0.5 # 利用一年242天数据,估计分数阶差分阶数
#d = calcHurst(np.log(RV)) – 0.5 # 利用一年242天数据,估计分数阶差分阶数
RV_log_d,g = calcy_d(np.log(RV),d) # 取对数 差分
# auto_arima(RV_log_d[0:242],start_p=0,start_q=0,max_p=2,max_q=0,d=1) # 模型自动定阶 根据AIC准则
model = ARIMA(RV_log_d[0:len_year1],order=(1,0,0)).fit() # 拟合模型(1-theta_1 *L) (x_t – theta_0) =e_t
# 获取估计系数
ar1 = model.params[1] #theta_1
const = model.params[0]*(1-ar1) #theta_0 * (1- theta_1)
len_day = len(data_day[‘year_high’])
ar_coef = []
a1 = ar1 – g[1]
ar_coef.append(a1)
for i in range(1,len_day):
a2 = ar1*g[i] – g[i+1]
ar_coef.append(a2)
RV_pre_arfima = []#基于ARFIMA模型RV
for i in range(len_day – len_year1):
#re_coef = ar_coef[0:i+1+len_year1] #提取分数阶差分系数
re_coef = ar_coef[0:50] #提取分数阶差分系数
#yii =list(np.log(RV[0:i+1+len_year1])) #提取时间序列RV的子样本,并且保存为列表
yii =list(np.log(RV[i+1+len_year1-50:i+1+len_year1])) #提取时间序列RV的子样本,并且保存为列表
yii.reverse()#将yii给逆序
log_pre = const + np.array(re_coef).dot(np.array(yii))#预测未来一天的对数RV
RV_pre_arfima.append(np.exp(log_pre))#将对数RV转化为RV
print(ar1)
print(np.mean(np.log(RV)))
print(const)
#print(RV_pre_arfima[1:242])
#print(RV[242:500])
RV_real = RV[len_year1:len(RV)]#实际已实现波动率,与预测的已实现波动率的时间一致
sig_RV_arfima = [(len_year1*x) ** 0.5 for x in RV_pre_arfima] #年华波动率
sig_RV_real = [(len_year1*x) ** 0.5 for x in RV_real] #年华波动率
#print(RV_real)
a= (np.array(RV_real)*len_year1)**0.5
print(a.round(4))
from statsmodels.tsa.arima.model import ARIMA
# from statsmodels.tsa.arima_model import ARMA
from pmdarima.arima import auto_arima
d = calcHurst(np.log(RV_week[0:len_year1-4])) – 0.5 # 利用一年242天数据,共242-4 个RV_week数据估计分数阶差分阶数
RV_week_log, g = calcy_d(np.log(RV_week),d) # 取对数 差分
# auto_arima(RV_week_log_d[0:242],start_p=0,start_q=0,max_p=2,max_q=0,d=1)
print(d)
print(g)
model = ARIMA(RV_week_log[0:len_year1-4],order=(1,0,0)).fit() # 拟合模型(1-theta_1 *L) (x_t – theta_0) =e_t
# 获取估计系数
ar1 = model.params[1] #theta_1
const = model.params[0]*(1-ar1) #theta_0 * (1- theta_1)
model = ARIMA(RV_week_log[0:len_year1 – 4], order=(1, 0, 0)).fit() # 拟合模型(1-theta_1 *L) (x_t – theta_0) =e_t
# 获取估计系数
ar1 = model.params[1] # theta_1
const = model.params[0] * (1 – ar1) # theta_0 * (1- theta_1)
len_day = len(data_day[‘year_high’])
ar_coef = []
a1 = ar1 – g[1]
ar_coef.append(a1)
for i in range(1, len(g) – 1):
a2 = ar1 * g[i] – g[i + 1]
ar_coef.append(a2)
RV_week_pre_arfima = [] # 基于ARFIMA模型RV
for i in range(len_day – len_year1):
# re_coef = ar_coef[0:i+1+len_year1] #提取分数阶差分系数
re_coef = ar_coef[0:50] # 提取分数阶差分系数
# yii =list(np.log(RV[0:i+1+len_year1])) #提取时间序列RV的子样本,并且保存为列表
yii = list(np.log(RV_week[i + 1 + len_year1 – 50 – 4:i + 1 + len_year1 – 4])) # 提取时间序列RV的子样本,并且保存为列表
yii.reverse() # 将yii给逆序
log_pre = const + np.array(re_coef).dot(np.array(yii)) # 预测未来一天的对数RV
RV_week_pre_arfima.append(np.exp(log_pre)) # 将对数RV转化为RV
RV_week_real = RV_week[len_year1-4:len(RV_week)]
sig_RV_week_arfima = [(len_year1*x) ** 0.5 for x in RV_week_pre_arfima]
sig_RV_week_real = [(len_year1*x) ** 0.5 for x in RV_week_real]
print(len(sig_RV_week_arfima))
print(len(sig_RV_week_real))
# 计算RV_mon
RV_mon = []
for i in range(len(RV)-21):
rv_mon = sum(RV[i:(22+i)]) / 22
RV_mon.append(rv_mon)
d = calcHurst(np.log(RV_mon[0:len_year1-21])) – 0.5# 利用一年242天数据,共242-21 个RV_mon数据估计分数阶差分阶数
RV_mon_log_d,g = calcy_d(np.log(RV_mon),d) # 取对数 差分
# auto_arima(RV_mon_log_d[0:242],start_p=0,start_q=0,max_p=2,max_q=0,d=1)
print(d)
print(g)
model = ARIMA(RV_mon_log_d[0:len_year1-21],order=(1,0,0)).fit() # 拟合模型(1-theta_1 *L) (x_t – theta_0) =e_t
# 获取估计系数
ar1 = model.params[1] #theta_1
const = model.params[0]*(1-ar1) #theta_0 * (1- theta_1)
len_day = len(data_day[‘year_high’])
ar_coef = []
a1 = ar1 – g[1]
ar_coef.append(a1)
for i in range(1,len(g)-1):
a2 = ar1*g[i] – g[i+1]
ar_coef.append(a2)
RV_mon_pre_arfima = []#基于ARFIMA模型RV
for i in range(len_day – len_year1):
#re_coef = ar_coef[0:i+1+len_year1] #提取分数阶差分系数
re_coef = ar_coef[0:50] #提取分数阶差分系数
#yii =list(np.log(RV[0:i+1+len_year1])) #提取时间序列RV的子样本,并且保存为列表
yii =list(np.log(RV_mon[i+1+len_year1-50-21:i+1+len_year1-21])) #提取时间序列RV的子样本,并且保存为列表
yii.reverse()#将yii给逆序
log_pre = const + np.array(re_coef).dot(np.array(yii))#预测未来一天的对数RV
RV_mon_pre_arfima.append(np.exp(log_pre))#将对数RV转化为RV
RV_mon_real = RV_mon[len_year1-21:len(RV_mon)]
sig_RV_mon_arfima = [(len_year1*x) ** 0.5 for x in RV_mon_pre_arfima]
sig_RV_mon_real = [(len_year1*x) ** 0.5 for x in RV_mon_real]
print(len(sig_RV_mon_arfima))
print(len(sig_RV_mon_real))
# 计算RV_3mon
RV_3mon = []
for i in range(len(RV) – 65):
rv_3mon = sum(RV[i:(66 + i)]) / 66
RV_3mon.append(rv_3mon)
d = calcHurst(np.log(RV_3mon[0:len_year1-65])) – 0.5 # 利用一年242天数据,共242-65 个RV_3mon数据估计分数阶差分阶数
RV_3mon_log_d,g = calcy_d(np.log(RV_3mon),d) # 取对数 差分
# auto_arima(RV_3mon_log_d[0:242],start_p=0,start_q=0,max_p=2,max_q=0,d=1)
print(d)
print(g)
model = ARIMA(RV_3mon_log_d[0:len_year1-65],order=(1,0,0)).fit() # 拟合模型(1-theta_1 *L) (x_t – theta_0) =e_t
# 获取估计系数
ar1 = model.params[1] #theta_1
const = model.params[0]*(1-ar1) #theta_0 * (1- theta_1)
len_day = len(data_day[‘year_high’])
ar_coef = []
a1 = ar1 – g[1]
ar_coef.append(a1)
for i in range(1,len(g)-1):
a2 = ar1*g[i] – g[i+1]
ar_coef.append(a2)
RV_3mon_pre_arfima = []#基于ARFIMA模型RV
for i in range(len_day – len_year1):
#re_coef = ar_coef[0:i+1+len_year1] #提取分数阶差分系数
re_coef = ar_coef[0:50] #提取分数阶差分系数
yii =list(np.log(RV_3mon[i+1+len_year1-50-65:i+1+len_year1-65])) #提取时间序列RV_3mon的子样本,并且保存为列表
yii.reverse()#将yii给逆序
log_pre = const + np.array(re_coef).dot(np.array(yii))#预测未来一天的对数RV
RV_3mon_pre_arfima.append(np.exp(log_pre))#将对数RV_3mon转化为RV_3mon
RV_3mon_real = RV_3mon[len_year1-65:len(RV_3mon)]
sig_RV_3mon_arfima = [(len_year1*x) ** 0.5 for x in RV_3mon_pre_arfima]
sig_RV_3mon_real = [(len_year1*x) ** 0.5 for x in RV_3mon_real]
print(len(sig_RV_3mon_arfima ))
print(len(sig_RV_3mon_real))
# 上述代码得到的一些结果
price = data_low
”’
data_low
sig_RV_arfima
sig_RV_week_arfima
sig_RV_mon_arfima
sig_RV_3mon_arfima
sig_ma_his
sig_RV_real
sig_RV_week_real
sig_RV_mon_real
sig_RV_3mon_real
sig_ma_real
”’
#print(n_sig_RV_arfima)
print(n_sig_RV_real)
n_sig_ma_real = np.array(n_sig_ma_real)
n_sig_ma_his = np.array(n_sig_ma_his)
maep_sigma = np.mean(abs(n_sig_ma_real – n_sig_ma_his)/n_sig_ma_real)#预测误差MAE
n_sig_RV_real = np.array(n_sig_RV_real)
n_sig_RV_arfima = np.array(n_sig_RV_arfima)
maep_RV = np.mean(abs(n_sig_RV_real – n_sig_RV_arfima)/n_sig_RV_real)#预测误差MAE
n_sig_RV_week_real = np.array(n_sig_RV_week_real)
n_sig_RV_week_arfima = np.array(n_sig_RV_week_arfima)
maep_RV_week = np.mean(abs(n_sig_RV_week_real – n_sig_RV_week_arfima)/n_sig_RV_week_real)#预测误差MAE
maep_sigma,maep_RV,maep_RV_week
choi_sig_RV_real = [(len_year1*x) ** 0.5 for x in RV][len(RV)-len(sig_RV_3mon_real)-len_year1 : len(RV)]
choi_sig_RV_week_real = [(len_year1*x) ** 0.5 for x in RV_week][len(RV_week)-len(sig_RV_3mon_real)-len_year1 : len(RV_week)]
choi_sig_RV_mon_real = [(len_year1*x) ** 0.5 for x in RV_mon][len(RV_mon)-len(sig_RV_3mon_real)-len_year1 : len(RV_mon)]
choi_sig_RV_3mon_real = [(len_year1*x) ** 0.5 for x in RV_3mon][len(RV_3mon)-len(sig_RV_3mon_real)-len_year1 : len(RV_3mon)]
choi_sig_ma_real = sig_ma_real[len(sig_ma_real)-len(sig_RV_3mon_real)-len_year1 : len(sig_ma_real)]
choi_sig_RV_real = [(len_year1*x) ** 0.5 for x in RV][len(RV)-len(sig_RV_3mon_real) : len(RV)]#将波动率给予年华
choi_sig_RV_week_real = [(len_year1*x) ** 0.5 for x in RV_week][len(RV_week)-len(sig_RV_3mon_real) : len(RV_week)]#将波动率给予年华
choi_sig_RV_mon_real = [(len_year1*x) ** 0.5 for x in RV_mon][len(RV_mon)-len(sig_RV_3mon_real) : len(RV_mon)]#将波动率给予年华
choi_sig_RV_3mon_real = [(len_year1*x) ** 0.5 for x in RV_3mon][len(RV_3mon)-len(sig_RV_3mon_real) : len(RV_3mon)]#将波动率给予年华
choi_sig_ma_real = sig_ma_real[len(sig_ma_real)-len(sig_RV_3mon_real) : len(sig_ma_real)]#将波动率给予年华
print(len(RV),len(RV_week),len_year1)
len(sig_ma_real)-len(sig_RV_week_real)-len_year1
print(len(choi_sig_ma_real))
print(len(choi_sig_RV_week_real))
print(len(choi_sig_RV_real))
#print(len(sig_RV_3mon_real))
path1 = “J:\”
path2 = “J:\”
path3 = “J:\”
# 保存数据 保留标题 不保留索引
n_date_low.to_csv(path1+’date.csv’,index=False,header=True,encoding=’gbk’)#保存低频日期,且文件名为date
n_price.to_csv(path1+’price.csv’,index=False,header=True,encoding=’gbk’)
n_sig_RV_arfima_df = pd.DataFrame(columns=[‘sig_RV_arfima’],data=n_sig_RV_arfima)
n_sig_RV_arfima_df.to_csv(path2+’sig_RV_arfima.csv’,index=False,header=True,encoding=’gbk’)
n_sig_RV_real_df = pd.DataFrame(columns=[‘sig_RV_real’],data=n_sig_RV_real)
n_sig_RV_real_df.to_csv(path2+’sig_RV_real.csv’,index=False,header=True,encoding=’gbk’)
n_sig_RV_week_arfima_df = pd.DataFrame(columns=[‘sig_RV_week_arfima’],data=n_sig_RV_week_arfima)
n_sig_RV_week_arfima_df.to_csv(path2+’sig_RV_week_arfima.csv’,index=False,header=True,encoding=’gbk’)
n_sig_RV_week_real_df = pd.DataFrame(columns=[‘sig_RV_week_real’],data=n_sig_RV_week_real)
n_sig_RV_week_real_df.to_csv(path2+’sig_RV_week_real.csv’,index=False,header=True,encoding=’gbk’)
n_sig_ma_his_df = pd.DataFrame(columns=[‘sig_ma_his’],data=n_sig_ma_his)
n_sig_ma_his_df.to_csv(path2+’sig_ma_his.csv’,index=False,header=True,encoding=’gbk’)
n_sig_ma_real_df = pd.DataFrame(columns=[‘sig_ma_real’],data=n_sig_ma_real)
n_sig_ma_real_df.to_csv(path2+’sig_ma_real.csv’,index=False,header=True,encoding=’gbk’)
sig_RV_arfima_df = pd.DataFrame(columns=[‘sig_RV_arfima(10-17-all)’],data=sig_RV_arfima)
sig_RV_arfima_df.to_csv(path2+’sig_RV_arfima(10-17-all).csv’,index=False,header=True,encoding=’gbk’)
sig_RV_week_arfima_df = pd.DataFrame(columns=[‘sig_RV_week_arfima(10-17-all)’],data=sig_RV_week_arfima)
sig_RV_week_arfima_df.to_csv(path2+’sig_RV_week_arfima(10-17-all).csv’,index=False,header=True,encoding=’gbk’)
sig_ma_his_df = pd.DataFrame(columns=[‘sig_ma_his(10-17-all)’],data=sig_ma_his)
sig_ma_his_df.to_csv(path2+’sig_ma_his(10-17-all).csv’,index=False,header=True,encoding=’gbk’)
choi_sig_RV_real_df = pd.DataFrame(columns=[‘choi_sig_RV_real’],data=choi_sig_RV_real)
choi_sig_RV_real_df.to_csv(path3+’choi_sig_RV_real.csv’,index=False,header=True,encoding=’gbk’)
choi_sig_RV_week_real_df = pd.DataFrame(columns=[‘choi_sig_RV_week_real’],data=choi_sig_RV_week_real)
choi_sig_RV_week_real_df.to_csv(path3+’choi_sig_RV_week_real.csv’,index=False,header=True,encoding=’gbk’)
choi_sig_ma_real_df = pd.DataFrame(columns=[‘choi_sig_ma_real’],data=choi_sig_ma_real)
choi_sig_ma_real_df.to_csv(path3+’choi_sig_ma_real.csv’,index=False,header=True,encoding=’gbk’)
PART3:作图
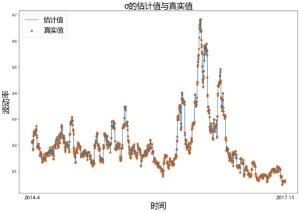
# 中文显示 plt.rcParams['font.sans-serif'] = ['Microsoft YaHei'] plt.figure(figsize=(15,10)) x = np.linspace(0,len(n_sig_ma_his),len(n_sig_ma_his)) color1 = [35/255,121/255,182/255] color2 = [254/255,104/255,3/255] plt.plot(x,n_sig_ma_his,color=color1,label='估计值') plt.scatter(x,n_sig_ma_real,color=color2,label='真实值')
# 设置横轴、纵轴、标题标签
plt.xlabel(‘时间’,fontsize=24)
plt.ylabel(‘波动率’,fontsize=24)
plt.title(‘σ的估计值与真实值’,fontsize=24)
# 设置x轴刻度
plt.xticks([0,len(n_sig_ma_his)],[‘2014.4′,’2017.11’],fontsize=15)
# 设置图例
plt.rcParams.update({‘font.size’: 20}) #设置图例字体大小
plt.legend(loc=’upper left’) # loc-图例位置
plt.show()
plt.figure(figsize=(15,10))
x = np.linspace(0,len(n_sig_RV_arfima),len(n_sig_RV_arfima))
color1 = [35/255,121/255,182/255]
color2 = [254/255,104/255,3/255]
plt.plot(x,n_sig_RV_arfima,color=color1,label=’预测值’)
plt.scatter(x,n_sig_RV_real,color=color2,label=’真实值’)
# 设置横轴、纵轴、标题标签
plt.xlabel(‘时间’,fontsize=24)
plt.ylabel(‘波动率’,fontsize=24)
plt.title(‘RV的预测值与真实值’,fontsize=24)
# 设置x轴刻度
plt.xticks([0,len(n_sig_RV_arfima)],[‘2014.4′,’2017.11’],fontsize=15)
# 设置图例
plt.rcParams.update({‘font.size’: 20}) #设置图例字体大小
plt.legend(loc=’upper left’) # loc-图例位置
plt.show()
plt.figure(figsize=(15,10))
x = np.linspace(0,len(n_sig_RV_week_arfima),len(n_sig_RV_week_arfima))
color1 = [35/255,121/255,182/255]
color2 = [254/255,104/255,3/255]
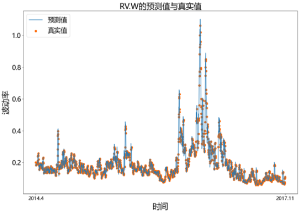
plt.plot(x,n_sig_RV_week_arfima,color=color1,label=’预测值’)
plt.scatter(x,n_sig_RV_week_real,color=color2,label=’真实值’)
# 设置横轴、纵轴、标题标签
plt.xlabel(‘时间’,fontsize=24)
plt.ylabel(‘波动率’,fontsize=24)
plt.title(‘RV.W的预测值与真实值’,fontsize=24)
# 设置x轴刻度
plt.xticks([0,len(n_sig_RV_week_arfima)],[‘2014.4′,’2017.11’],fontsize=15)
# 设置图例
plt.rcParams.update({‘font.size’: 20}) #设置图例字体大小
plt.legend(loc=’upper left’) # loc-图例位置
plt.show()
plt.figure(figsize=(15,10))
x = np.linspace(0,len(n_sig_RV_mon_arfima),len(n_sig_RV_mon_arfima))
color1 = [35/255,121/255,182/255]
color2 = [254/255,104/255,3/255]
plt.plot(x,n_sig_RV_mon_arfima,color=color1,label=’预测值’)
plt.scatter(x,n_sig_RV_mon_real,color=color2,label=’真实值’)
# 设置横轴、纵轴、标题标签
plt.xlabel(‘时间’,fontsize=24)
plt.ylabel(‘波动率’,fontsize=24)
plt.title(‘RV.M的预测值与真实值’,fontsize=24)
# 设置x轴刻度
plt.xticks([0,len(n_sig_RV_mon_arfima)],[‘2014.4′,’2017.11’],fontsize=15)
# 设置图例
plt.rcParams.update({‘font.size’: 20}) #设置图例字体大小
plt.legend(loc=’upper left’) # loc-图例位置
plt.show()
plt.figure(figsize=(15,10))
x = np.linspace(0,len(n_sig_RV_3mon_arfima),len(n_sig_RV_3mon_arfima))
color1 = [35/255,121/255,182/255]
color2 = [254/255,104/255,3/255]
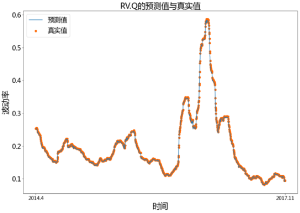
plt.plot(x,n_sig_RV_3mon_arfima,color=color1,label=’预测值’)
plt.scatter(x,n_sig_RV_3mon_real,color=color2,label=’真实值’)
# 设置横轴、纵轴、标题标签
plt.xlabel(‘时间’,fontsize=24)
plt.ylabel(‘波动率’,fontsize=24)
plt.title(‘RV.Q的预测值与真实值’,fontsize=24)
# 设置x轴刻度
plt.xticks([0,len(n_sig_RV_3mon_arfima)],[‘2014.4′,’2017.11’],fontsize=15)
# 设置图例
plt.rcParams.update({‘font.size’: 20}) #设置图例字体大小
plt.legend(loc=’upper left’) # loc-图例位置
plt.show()



PART4:复制策略研究
M = 66
s = list(n_price.iloc[:,0].values) # 投资组合 PortD_D不同参数R_σ 、R_K的夏普率计算代码 choi_sig = list(choi_sig_RV_week_real.iloc[:, 0].values) sig = list(n_sig_RV_week_arfima.iloc[:, 0].values) ra2 = [0.05, 0.1, 0.15, 0.2, 0.25, 0.3] ra1 = np.linspace(0.6, 1, 50) sharp = np.zeros((50, 6)) for i in range(0, 6):
for j in range(0, 50):
print(‘i,j=’, i, j, end=’,’)
ratio2 = ra2[i]
ratio1 = ra1[j]
sharp[j, i] = sharpe_var(s, sig, choi_sig)[0]
path =”J:\sharp”
sharp_D_D = pd.DataFrame(columns=[‘0.05′,’0.1′,’0.15′,’0.2′,’0.25′,’0.3’],data=sharp)
sharp_D_D.to_csv(path+’sharp_D_D.csv’,index=False,header=True,encoding=’gbk’)
# PortD_RQ
choi_sig = list(choi_sig_ma_real.iloc[:,0].values)
sig =list(n_sig_RV_3mon_arfima.iloc[:,0].values)
ra2 = [0.05,0.1,0.15,0.2,0.25,0.3]#执行价格参数
ra1 = np.linspace(0.6,1,200)#市场进入参数
sharp = np.zeros((200,6))
for i in range(0,6):
for j in range(0,200):
ratio2 = ra2[i]
ratio1 = ra1[j]
sharp[j,i] = sharpe_var(s,sig,choi_sig)[0]
sharp_D_RQ = pd.DataFrame(columns=[‘0.05′,’0.1′,’0.15′,’0.2′,’0.25′,’0.3’],data=sharp)
sharp_D_RQ.to_csv(path+’sharp_D_RQ.csv’,index=False,header=True,encoding=’gbk’)
# PortRQ_RM
choi_sig = list(choi_sig_RV_3mon_real.iloc[:,0].values)
sig = list(n_sig_RV_mon_arfima.iloc[:,0].values)
ra2 = [0.05,0.1,0.15,0.2,0.25,0.3]
ra1 = np.linspace(0.6,1,200)
sharp = np.zeros((200,6))
for i in range(0,6):
for j in range(0,200):
ratio2 = ra2[i]
ratio1 = ra1[j]
sharp[j,i] = sharpe_var(s,sig,choi_sig)[0]
sharp_RQ_RM = pd.DataFrame(columns=[‘0.05′,’0.1′,’0.15′,’0.2′,’0.25′,’0.3’],data=sharp)
sharp_RQ_RM.to_csv(path+’sharp_RQ_RM.csv’,index=False,header=True,encoding=’gbk’)
# PortRQ_RQ
choi_sig = list(choi_sig_RV_3mon_real.iloc[:,0].values)
sig = list(n_sig_RV_3mon_arfima.iloc[:,0].values)
ra2 = [0.05,0.1,0.15,0.2,0.25,0.3]
ra1 = np.linspace(0.6,1,200)
sharp = np.zeros((200,6))
for i in range(0,6):
for j in range(0,200):
ratio2 = ra2[i]
ratio1 = ra1[j]
sharp[j,i] = sharpe_var(s,sig,choi_sig)[0]
sharp_RQ_RQ = pd.DataFrame(columns=[‘0.05′,’0.1′,’0.15′,’0.2′,’0.25′,’0.3’],data=sharp)
sharp_RQ_RQ.to_csv(path+’sharp_RQ_RQ.csv’,index=False,header=True,encoding=’gbk’)
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
# 中文显示
plt.rcParams[‘font.sans-serif’] = [‘Microsoft YaHei’]
path = “J:\sharp”
sharp = pd.read_csv(path+’sharp_D_D.csv’,encoding=’gbk’)
plt.figure(figsize = (10,6))
x = np.linspace(0.6,1,50)
# 绘制曲线图
plt.plot(x,sharp.iloc[:,0],color = ‘k’,label = ‘Rk=0.05′, ls=’-‘) # 黑色 实线
plt.plot(x,sharp.iloc[:,1],color = ‘r’,label = ‘Rk=0.1′, ls=’–‘) # 红色 虚线
plt.plot(x,sharp.iloc[:,2],color = ‘g’,label = ‘Rk=0.15′, ls=’:’) # 绿色 点线
plt.plot(x,sharp.iloc[:,3],color = ‘b’,label = ‘Rk=0.2′, ls=’-.’) # 蓝色 点虚线
plt.plot(x,sharp.iloc[:,4],color = ‘pink’,label = ‘Rk=0.25′, marker=’*’) # 粉色 星号线
plt.plot(x,sharp.iloc[:,5],color = ‘c’,label = ‘Rk=0.3′, marker=’+’) # 青色 加号线
plt.axhline(0,c=’b’,ls=’–‘)
# 设置横纵轴和标题
plt.title(‘市场时机参数Rσ与执行价格Rk对策略PortBPW_RW夏普比的影响’,fontsize=24)
plt.xlabel(‘市场进入时机参数Rσ’,fontsize=24)
plt.ylabel(‘夏普比’,fontsize=24)
# 添加图例
plt.legend(loc=’lower right’) # loc-图例位置
Garch模型的在险价值Var估计
import pandas as pd
import numpy as np
from arch import arch_model
import datetime as dt
import scipy.stats as stats
import warnings
warnings.filterwarnings('ignore')
# 数据读取与预处理
data = pd.read_excel('上证综合指数日数据(2016年-2021年).xlsx')
data['交易日期'] = pd.to_datetime(data['交易日期'])
data_part = data[(data['交易日期'] > '01/01/2016') & (data['交易日期'] <= '12/31/2018')]
r_part = data_part['指数回报率']
# RiskMetrics模型参数初始化
Vol_RM = []
date_pre = data[(data['交易日期'] > '01/01/2019')].iloc[:, 1]
returns_pre = data[(data['交易日期'] > '01/01/2019')].iloc[:, 7]
var_r = np.var(r_part)
# 波动率预测与VaR计算
for i in date_pre:
r_day = data[data['交易日期'] == i].iloc[:, 7].values
vol_rm2 = 0.94 * var_r + 0.06 * r_day**2
Vol_RM.append(vol_rm2)
var_r = vol_rm2
# 模型拟合与分位数计算
am = arch_model(r_part, mean='zero', vol="Garch", p=1, o=0, q=1, dist="normal")
res = am.fix([0, 0.06, 0.94]) # 固定参数
q = am.distribution.ppf(0.99) # 标准正态分布99%分位数
VaR_RM = np.sqrt(Vol_RM) * q
# 结果存储
VaRs_RM = pd.DataFrame(columns={'交易日期'}, data=date_pre[1:])
VaRs_RM['VaR'] = VaR_RM[0: len(VaR_RM)-1]
VaRs_RM['实际收益率'] = returns_pre[1:]
# GARCH模型拟合
am2 = arch_model(r_part, mean='zero', vol="Garch", p=1, o=0, q=1, dist="normal")
res2 = am2.fit(disp='off')
q2 = am2.distribution.ppf(0.99) # 标准正态分布分位数
# 条件波动率提取
condi_vol = res2.conditional_volatility
resid_GARCH = res2.resid
condi_vol1 = condi_vol[len(condi_vol)-1]
# 波动率预测
Vol_Garch = []
var_r = condi_vol1**2
for i in date_pre:
r_day = data[data['交易日期'] == i].iloc[:, 7].values
vol_garch = omega + beta * var_r + alpha * r_day**2 # 参数需替换为实际估计值
Vol_Garch.append(vol_garch)
var_r = vol_garch
# VaR算与存储
VaR_GARCH = np.sqrt(Vol_Garch) * q2
VaRs_GARCH = pd.DataFrame(columns={'交易日期'}, data=date_pre[1:])
VaRs_GARCH['VaR'] = VaR_GARCH[0: len(VaR_GARCH)-1]
VaRs_GARCH['实际收益率'] = returns_pre[1:]
# t分布GARCH模型拟合
am3 = arch_model(r_part, mean='zero', vol="Garch", p=1, o=0, q=1, dist="t")
res3 = am3.fit(disp='off')
q3 = am3.distribution.ppf(0.01, paras[3]) # t分布1%分位数
# 波动率预测(同GARCH模型)
Vol_Garch = []
var_r = condi_vol1**2
for i in date_pre:
r_day = data[data['交易日期'] == i].iloc[:, 7].values
vol_garch = omega + beta * var_r + alpha * r_day**2
Vol_Garch.append(vol_garch)
var_r = vol_garch
# VaR计算与存储
VaR_GARCH = np.sqrt(Vol_Garch) * q3
VaRs_GARCH = pd.DataFrame(columns={'交易日期'}, data=date_pre[1:])
VaRs_GARCH['VaR'] = VaR_GARCH[0: len(VaR_GARCH)-1]
VaRs_GARCH['实际收益率'] = returns_pre[1:]
# 失败率计算
tau = 0.99
T = len(VaR_Garch)
N_RM, N_Garch = 0, 0
for i in date_pre:
if VaRs_GARCH[VaRs_GARCH['交易日期'] == i].iloc[:, 2].values < (-1) * VaRs_GARCH[VaRs_GARCH['交易日期'] == i].iloc[:, 1].values:
N_Garch += 1
if VaRs_RM[VaRs_RM['交易日期'] == i].iloc[:, 2].values < (-1) * VaRs_RM[VaRs_RM['交易日期'] == i].iloc[:, 1].values:
N_RM += 1
F_RM = N_RM / T
F_Garch = N_Garch / T
# Kupiec拟然比检验
LR_RM = 2 * (T - N_RM) * np.log((1 - F_RM) / tau) + 2 * N_RM * np.log(F_RM / (1 - tau))
LR_Garch = 2 * (T - N_Garch) * np.log((1 - F_Garch) / tau) + 2 * N_Garch * np.log(F_Garch / (1 - tau))
p_RM = 1 - stats.chi2.cdf(LR_RM, df=1)
p_Garch = 1 - stats.chi2.cdf(LR_Garch, df=1)
ADB连接模块
import os
import json
def get_mumu_info():
# 获取 Roaming AppData 目录
appdata = os.environ[‘APPDATA’]
mumu_config_path = os.path.join(appdata, “Netease”, “MuMuPlayer”, “install_config.json”)
mumu_share_path = os.path.join(appdata, “Netease”, “MuMuPlayer”, “vm_config.json”)
# 读取配置文件
with open(mumu_config_path, ‘r’, encoding=’utf-8′) as file:
config_data = json.load(file)
# 提取player部分的version和install_dir
player_version = config_data[‘player’][‘version’]
player_install_dir = config_data[‘player’][‘install_dir’]
# adb 路径
adb_path = os.path.join(player_install_dir, ‘adb.exe’)
# 读取共享文件夹JSON文件
with open(mumu_share_path, ‘r’, encoding=’utf-8′) as file:
share_data = json.load(file)
# 提取sharefolder部分的user里的path
sharefolder_user_path = share_data[‘vm’][‘sharefolder’][‘user’][‘path’]
# 定义图片保存目录
windows_image_save_dir = os.path.join(sharefolder_user_path, ‘Pictures’)
android_image_save_dir = ‘/sdcard/Pictures’
# 返回收集的信息
return {
“player_version”: player_version,
“player_install_dir”: player_install_dir,
“adb_path”: adb_path,
“sharefolder_user_path”: sharefolder_user_path,
“windows_image_save_dir”: windows_image_save_dir,
“android_image_save_dir”: android_image_save_dir
}
# 调用函数并打印结果
mumu_info = get_mumu_info()
print(f”版本: {mumu_info[‘player_version’]}”)
print(f”安装目录: {mumu_info[‘player_install_dir’]}”)
print(f”adb路径: {mumu_info[‘adb_path’]}”)
print(f”用户共享文件夹路径: {mumu_info[‘sharefolder_user_path’]}”)
print(f”Windows本地目录映射: {mumu_info[‘windows_image_save_dir’]}”)
print(f”安卓端目录映射: {mumu_info[‘android_image_save_dir’]}”)
ADB操作模块
mumu_info = get_mumu_info()
def start_mumu_adb_service():
current_dir = os.getcwd()
try:
# 切换工作目录
os.chdir(mumu_info['player_install_dir'])
# 执行连接命令
result = subprocess.run(['adb.exe', 'connect', '127.0.0.1:16384'], check=True, capture_output=True, text=True)
# 输出adb命令的结果
print("ADB连接结果:", result.stdout.strip())
# 切回原目录
os.chdir(current_dir)
return result.stdout.strip()
except Exception as e:
print(f"启动adb失败,请手动打开: {e}")
# 切回原目录
os.chdir(current_dir)
return []
start_mumu_adb_service()
def get_device_id():
"""
获取连接的模拟器的设备 ID 列表。
:return: 设备 ID 列表
"""
current_dir = os.getcwd()
try:
# 切换工作目录
os.chdir(mumu_info['player_install_dir'])
result = subprocess.run(['adb.exe', 'devices'], capture_output=True, text=True).stdout
device_ids = [line.split('t')[0] for line in result.split('n') if 'tdevice' in line]
# 切回原目录
os.chdir(current_dir)
return device_ids
except Exception as e:
print(f"获取设备ID失败: {e}")
# 切回原目录
os.chdir(current_dir)
return []
def click(device_ids, Area):
“””
模拟在设备上指定坐标点击。
:param x: 点击的 x 坐标
:param y: 点击的 y 坐标
“””
current_dir = os.getcwd()
x = Area[0]
y = Area[1]
try:
# 切换工作目录
os.chdir(mumu_info[‘player_install_dir’])
cmd = f’adb.exe -s {device_ids[0]} shell input tap {x} {y}’
subprocess.run(cmd, shell=True, check=True)
# 切回原目录
os.chdir(current_dir)
return True
except subprocess.CalledProcessError as e:
print(f”执行命令失败: {e}”)
except Exception as e:
print(f”发生错误: {e}”)
return False
个人优点
擅长逻辑思考,在数学方面较为突出,同时喜欢独立设计各种小规模系统和组装工业半成品
有快速学习和持续接受新知识的能力,能快速接受新任务交接
连续参与数学建模竞赛5天每天14小时
同时学习过金融学和数学两组体系,交叉应用。
部分摄影作品


2025年月全食的记录过程和结果
使用400-600MM镜头拍摄




岳麓山里的蘑菇







NICE
DAYS
IN
AUTUMN











给同学们上数学分析习题课